Пример организации системы физической защиты
Современное состояние проблемы обеспечения безопасности особо важных объектов определяется множеством факторов, в том числе и применением технических систем обеспечения охраны. Наиболее существенными из них являются применения интегрированных комплексов систем физической защиты, созданных на основе новых научно-технических разработок. Для оценки эффективности данных комплексов проводятся научно-исследовательские работы, направленные на улучшение или модернизацию СФЗ за счет оптимизации структуры или состава оборудования комплексов.
В ряде научных исследований, проводимых в ЗАО «КОМПАНИЯ БЕЗОПАСНОСТЬ», большое внимание уделено созданию моделей движения нарушителя и различных алгоритмов расчета параметров движения нарушителей, появившихся в районе нахождения защищаемых объектов контролируемой зоны.
Рассмотрим реализацию алгоритма расчета времени проникновения нарушителя на особо важный объект. Чтобы определить, выполняет ли система физической защиты свою функцию, необходимо оценить время прибытия к объекту защиты нарушителя или группы реагирования для последующего расчета минимального времени движения нарушителя до объекта защиты.
Для расчета определим математическую модель.
На план исследуемого объекта наносится поле, состоящее из Nx и Ny клеток, каждая из которых определяется вектором параметров:
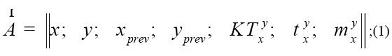
где:
x - координата точки по оси ox,
y - координата точки по оси oy,
xprev - координата точки по оси , из которой переместился в данную клетку нарушитель.
yprev - координата точки по оси , из которой переместился в данную клетку нарушитель.
KT - дискретное время преодоления клетки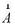 
,
t - минимальное дискретное время, через которое после начала расчета нарушитель может попасть в точку ,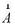
m - маркер, показывающий, что вероятный нарушитель прошел данную клетку (m=0), или не прошел (m=1).
Стартовая клетка определяется вектором параметров:
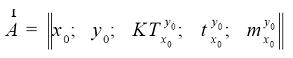
Так как стартовая клетка – точка начала движения нарушителя, то на первом дискрете времени необходимо указать, что нарушитель прошел данную клетку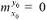 
. Данный маркер показывает, что в пройденную нарушителем клетку нельзя попасть второй раз, так как новое время прибытия нарушителя всегда будет больше предыдущего, а в рамках данной задачи мы ищем минимальное время. Таким образом, по приведенному алгоритму нельзя вернуться в исходную точку.
После того как нарушитель начал двигаться, не ясно в каком направлении ему необходимо пойти, так как самый короткий путь может оказаться в совершенно любом направлении. Поэтому нарушитель начинает двигаться сразу во все возможные направления, то есть в точки с координатами:
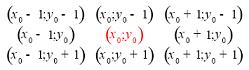
При этом необходимо проверять существование каждой точки из восьми возможных:
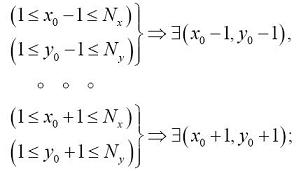
Итак, получен массив точек, в которые может попасть нарушитель из стартовой точки. Значение маркера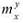 
во всех точках равно 1, поэтому, если точка существует, нарушитель может туда попасть. Нам остается только проверить, что время 
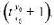, за которое нарушитель может попасть в данную клетку поля, меньше времени 
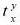, записанного там по умолчанию.
Если данное условие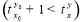 
не выполняется, то это означает, что данная клетка более не интересна для рассмотрения, так как путь через нее превышает по времени путь, полученный из кратчайшего расстояния до объекта защиты. Если же полученное время 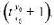оказалось меньше 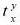, то нарушитель может попасть в данную клетку, а время, за которое он может туда попасть определяется, как .
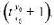Так как нарушитель перешел в соседние клетки, необходимо пометить все эти клетки маркером нарушителя: .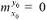
После перехода в одну из соседних клеток нам необходимо уменьшить время преодоления данной клетки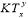 
на величину, равную t (2):
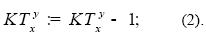
Если после уменьшения времени преодоления данной клетки 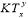на 1 окажется, что оно стало равно нулю, можно говорить о том, что данная клетка преодолена нарушителем и на следующем ходу он снова сможет пойти в ряд соседних клеток.
Клетки, в которых произошло обнуление времени преодоления, заносятся в массив «Fast». Все остальные клетки, в которых не произошло обнуления времени преодоления, заносятся в массив «Slow». В данных клетках нарушитель будет находиться до тех пор, пока время преодоления 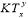не обнулится. Блок схема алгоритма приведена на рис. 1.
Массив «Fast» формируется из клеток, из которых на следующем шаге необходимо уходить в соседние клетки и состоит из векторов типа (1).
Для всех значений i необходимо произвести анализ, аналогичный анализу, проведенному для стартовой клетки. После перехода в одну из соседних клеток нам необходимо уменьшить время преодоления данной клетки на величину, равную дискрету времени D t (2).
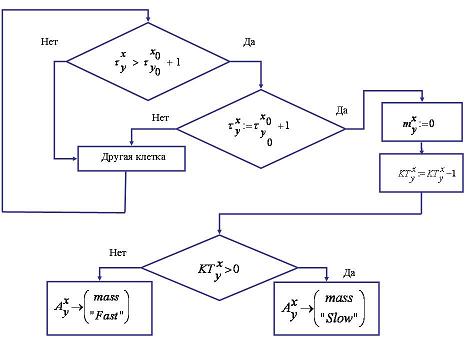
Рис.1 Алгоритм проведения расчета на первом шаге
Если после уменьшения времени преодоления данной клетки на 1 окажется, что оно стало равно нулю, можно говорить о том, что данная клетка преодолена нарушителем и на следующем ходу он снова сможет пойти в ряд соседних клеток. Клетки, в которых произошло обнуление времени преодоления, заносятся в массив «Fast». Блок схема алгоритма обработки i-го элемента массива «Fast» приведена на рис. 2. Проверку маркера 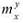осуществлять не нужно, так как нарушитель на данной итерации не может перейти в следующую клетку поля.
Массив «Slow» также состоит из векторов типа (1). В данной клетке необходимо уменьшить время ее преодоления на величину, равную дискрету времени D t (2).
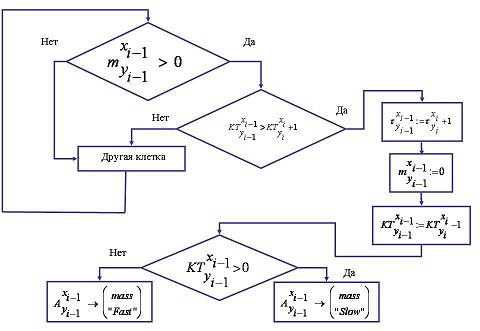
Рис.2 Обработка i-го элемента массива «Fast»
Если после уменьшения времени преодоления данной клетки на 1 окажется, что оно стало равно нулю, можно говорить о том, что данная клетка преодолена нарушителем и на следующем ходу он снова сможет пойти в ряд соседних клеток.
Клетки, в которых произошло обнуление времени преодоления, заносятся в массив «Fast». Все остальные клетки, в которых не произошло обнуления времени преодоления, остаются в массиве «Slow». В данных клетках нарушитель будет находиться до тех пор, пока время преодоления не обнулится. Блок схема алгоритма обработки i-го элемента массива «Slow» приведена на рис. 3.
Поиск завершится в тот момент, когда нарушитель по самому быстрому пути перейдет в клетку с вектором параметров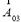 
, в которой расположен объект защиты. Используя параметры клеток xprev и yprev, можно восстановить весь путь движения нарушителя.
Таким образом, рассмотренный алгоритм расчета минимального времени проникновения нарушителя позволил определить, что система физической защиты выполняет свою функцию, оценивая, кто раньше прибудет к объекту защиты – нарушитель или группа реагирования.
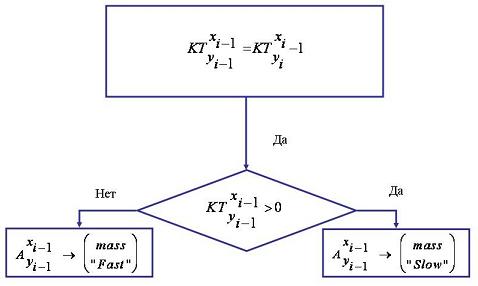
Рис.3 Обработка i-го элемента массива «Slow»
Сумма времен преодоления каждой клетки на полученном пути даст минимальное время проникновения нарушителя.
Однако, следует отметить, что расчет оказывается существенно заниженным и требуются дополнительные исследования, так как время преодоления клетки в диагональном направлении оказывается равным времени преодоления ее в горизонтальном или вертикальном направлениях.
УДК 654.94
Авторы: С.И. Корчагин
А.В. Леус
А.В. Филимонов
ЗАО "Компания Безопасность"
Авторы: С.И. Корчагин
А.В. Леус
А.В. Филимонов
ЗАО "Компания Безопасность"
Читайте также:
- Выбор модели движение нарушителя относительно наблюдаемых объектов ИК СФЗ в контролируемой зоне
- Общее предельное решение алгебраических уравнений
- Порядок проведения оптимизации структуры ИК СФЗ на основе выбора наиболее эффективных альтернативных вариантов
- Анализ и синтез математических моделей физических устройств и процессов
- Теория отображения алгебраических функций
