Одним из самых очевидных факторов, сформировавшихся в последнее десятилетие, является изменение характера угроз, вызванное активизацией деятельности внешних нарушителей по отношению к охраняемым особо важным объектам. Успех в достижении цели и решении задач физической защиты охраняемых особо важных объектов важное место занимают интегрированные комплексы СФЗ. Для оценки эффективности данных комплексов проводятся научно-исследовательские работы, направленные на улучшение или модернизацию СФЗ за счет оптимизации структуры или состава оборудования комплексов.
Модель движения нарушителя с математической точки зрения может носить либо качественный (вербальный) характер, либо количественный (описанный математически). Количественное описание ряда характеристик движения нарушителя является проблематичным. Общими подходами к описанию параметров движения формализованной модели являются вероятностный и детерминированный подходы.
Построение математической модели устанавливает связь между движением внешнего нарушителя, появившимся в районе нахождения защищаемых объектов контролируемой зоны, ИКСФЗ и измеряемыми параметрами движения нарушителя.
Так как требования к точности результатов решения задачи достаточно высоки, то возникает необходимость учитывать при построении математической модели особенности свойств нарушителя, процесса его движения и возможности систем ИК СФЗ по его обнаружению, распознаванию, идентификации и способности слежения при условии изменения параметров движения нарушителя.
При построении математической модели хорошо известны законы, определяющие поведение и свойства возможного нарушителя контролируемой зоны особо важных объектов, известны процессы в системах ИК СФЗ, и имеется большой практический опыт их применения.
В рамках вероятностного подхода к описанию параметров движения формализованной модели, наиболее полным математическим описанием движения нарушителя является многомерный случайный вектор Н. Отдельные характеристики (вооруженность, подготовленность и т. д.) нарушителя в этом случае описываются дифференциальными распределениями значений характеристик и их корреляционной матрицей.
При таком описании показатели эффективности ИКСФЗ получают с помощью имитационного моделирования на множестве реализаций взаимодействия нарушителя с ИК СФЗ защищаемого объекта. Имитационное моделирование реализуется в методе статистических испытаний (его часто называют методом Монте-Карло).
Основная идея метода статистических испытаний состоит в том, что вероятностные характеристики различных сложных случайных процессов, описывающих функционирование систем, могут быть рассчитаны с помощью имитационных моделей даже в тех случаях, когда аналитически это сделать не представляется возможным или затруднительно.
Искомая вероятность может быть легко оценена методом статистических испытаний. Технология расчета осуществляется по кривой W=f(r) изображена на рисунке 1. Здесь абсцисса выбрана так, чтобы значение f(a) было достаточно малым (например, 0,001), а ордината b равна f(max). Теперь понятно, что расчет вероятности P эквивалентен вычислению площади S под кривой W=f(r), при r принадлежащей [0;a].
Пусть в прямоугольнике с координатами вершин [0;0], [0;b], [a;0], [a;b] формируется точка, координаты которой случайны и независимы, причем абсцисса равномерно распределена в P, а ордината равномерно распределена в [0;b] (рис. 1).
Вероятность попадания этой точки в область под кривой P равна площади под кривой W=f(r), то есть искомой вероятности. С другой стороны эту вероятность легко оценить, если провести испытаний, подсчитать количество попаданий точки в область под кривой и вычислить отношение.
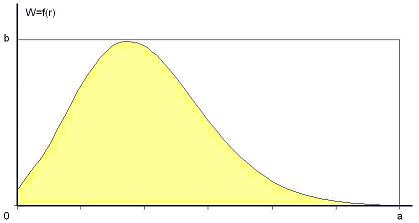
Рис.1 График зависимости W=f(r)
Легко показать, что оценка v является несмещенной и состоятельной оценкой P. С другой стороны вероятность легко оценить, если провести n испытаний, подсчитать количество k попаданий точки в область под кривой и вычислить отношение:
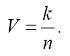
Действительно, если вероятность какого-либо события нужно оценить так, чтобы дисперсия оценки не превосходила заданного числа, то требуемое число опытов определяется неравенством
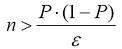
Таким образом, для расчета искомой вероятности достаточно иметь датчики равномерно распределенных случайных величин. Однако обоснование видов законов распределения соответствующих случайных величин, определение их параметров и корреляционной матрицы требуют огромного числа статистических данных, которые, как правило, отсутствуют.
При детерминированном подходе в качестве параметров движения внешнего нарушителя выбирают отдельные точки дифференциальных законов распределения случайных величин для характеристик рассматриваемого нарушителя.
В качестве таких точек обычно рассматривают максимально возможные, наиболее вероятные значения либо значения, реализующиеся с некоторой заранее заданной вероятностью. Эти точки определяются экспертно по диапазону возможных значений, известному из анализа происходивших противоправных действий в отношении особо важных объектов рассматриваемого типа.
Для получения приближенного решения необходимо принять ряд дополнительных допущений используемых в дальнейшем при рассмотрении движения нарушителя в условиях существующего рельефа местности и действия атмосферы, влияющих на особенности работы ИК СФЗ:
- особенностей рельефа местности и «фонирования» грунтов;
- стандартных климатических условий для данной местности нахождения особо важного объекта, метеорологических и геофизических факторов в данное время года, которые и определяют выбор оборудования при построении ИК СФЗ.
- изменений плотности воздуха при барометрической высоте нахождения объекта защиты;
- кривизне поверхности Земли.
Это связано с тем, что расстояния точки появления нарушителя в контролируемой зоне до объекта защиты может быть соизмеримо с расстоянием от места нахождения сил противодействия нарушителю до объекта защиты или меньше данного расстояния.
При анализе эффективности ИК СФЗ для крупных и сложных объектов, не исключается ситуация, когда отдельные пути проникновения и реализации угроз просто не будут приняты к рассмотрению из-за субъективной ошибки экспертной комиссии, что в конечном итоге приведёт к неоправданному завышению оценки эффективности СФЗ объекта.
Возникает необходимость иметь способ оценки эффективности ИКСФЗ на основе математической модели, который будет:
- свободным от воздействия субъективных факторов при проведении оценки эффективности;
- автоматически определять оптимальный маршрут движения нарушителя (включая точку начала и завершения движения);
- автоматически определять время движения нарушителя (с учетом преодоления им физических барьеров) и время движения сил охраны объекта;
- реагировать (путем изменения маршрутов и времен движения нарушителя и сил охраны объекта) на изменение состава инженерных и технических средств, входящих в ИК СФЗ.
- вероятность пресечения НСД;
- вероятность нейтрализации нарушителей;
- вероятность своевременного перехвата нарушителей;
- вероятность то или иного исхода бой – столкновения;
- вероятность проявления различных рисков и другие.
Необходимо учитывать и разброс возможных значений параметров модели. Следовательно, в рамках данного подхода, лучше использовать комбинированную модель, сочетающую элементы качественного и количественного описания вероятностного и детерминированного подходов.
ЗАО "Компания Безопасность"
- Теория отображения алгебраических функций
- Реализация алгоритма для расчета минимального времени проникновения нарушителя
- Порядок проведения оптимизации структуры ИК СФЗ на основе выбора наиболее эффективных альтернативных вариантов
- Алгебраические уравнения
- Аналитический синтез и анализ математических моделей



